

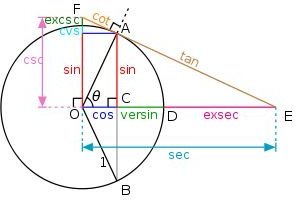
The sheets are protected so someone does not "accidentally" enter an angle in the wrong cell on the wrong spreadsheet, but there is no password if you wish to unprotect it. In one sheet, you can enter your angles in degrees, in another, you enter you angles in radians, and in the third, you can enter your angles as mulitples of pi radians (since so much of early trig focuses on "simple" angles like pi*1/3 or pi*3/4 or pi*1). The attached spreadsheet is a relatively simple attempt to illustrate the unit circle and the basic trig functions. She struggled with trig until she finally grasped the unit circle. It was gratifying when she came back and said that it was true. When my oldest child was starting to learn trig, I encouraged her to work hard to understand the unit circle when it came up, and the rest of trig would be a lot easier. I don’t write any of that out but that is what’s going on behind the scenes when I’m trying to evaluate trig.I recall back when I was first learning trig how much more things made sense once I had a solid grasp of the unit circle. I’m in the second quadrant so y is positive and x is negative. Counting by pi/6, I’m pointing straight up at 3pi/6=pi/2, so 4pi/6=2pi/3 is just a little past it. I’d think of it as 4pi/6 because it makes the counting easier. Once you know those, you just have to figure out which situation you’re in, whether the vertical length or the horizontal length is longer (only necessary for pi/6 or pi/3 variants), and which quadrant you are in to determine sign.įor example, consider 2pi/3. Solve for the last side using the Pythagorean theorem again. That gives you a hypotenuse of 1 on the original triangle and shows the shorter side must be 1/2. Put two of those side-by-side to form an equilateral triangle with side lengths of 1. Variants of pi/6 or pi/3 are 30-60-90 triangles.

Using the fact that both legs are the same allows you to get those lengths. The triangles come into play because the radius of the unit circle becomes the hypotenuse of a triangle with one leg being an x-length and the other a y-length.Īny variant of pi/4 is just using the Pythagorean theorem on a 45-45-90 triangle with a hypotenuse of 1. Basically, the cosine gives you the x-coordinate and sine the y-coordinate of a point on the unit circle. If you feel like you’re memorizing the common angles, find a derivation for those.


 0 kommentar(er)
0 kommentar(er)
